
An implicit
function is an equation containing both x and y variable, and every solution
(for x and y) of this equation is a part of the graph.
For instance, the equation of a simple circle would be: x^2+y^2=1. All (x;y)
points satisfying this equation are on the graph of this function, which is a
circle centered at (0;0) and of radius one.
Putting the whole equation in the left part of the equation (at the left of the "=") makes a function f(x,y)=0.
You can very easily turn an explicit ( y=f(x) ) equation into implicit form: f(x)-y=0.
picFX lets you "enlight" the graph of any implicit equation. Look at the steps below:
1) First adapt
your equation so that it suits your project (remember that x goes from zero to
the width of the project, usually 255; y does the same)
Once you have your equation f(x,y)=0, we will work on the left expression and
forget about the "=0".
2) Since f(x,y)
can be either negative or positive, raise it to square (unnecessary if you're
sure that it will never happen). You will then have f(x,y)^2.
[You can try rendering your function here. It is usually some chaothic stuff,
but you will sometimes get some interesting results]
3) Now add a
constant [We'll name it k]. Depending how "steep" your function is
near its zeros, that constant may have to be quite big (upto one million
sometimes).
You will anyway have to change this constant once it is finished, so that the
result suits your needs.
Now we are sure that the function is always equal to or bigger than this
constant.
f(x,y)^2+k
4) Let's do now the inverse of this function (It will be very small, except near the places where the original function is near zero, where it will get near 1/k).
1/(f(x,y)^2+k)
5) To use the full [0-255] range, multiply by k*255
k*255/(f(x,y)^2+k)
Ok. Now you know how to do it, you may either try it at once (If you can't wait ;-) or do what I suggest step by step.
Let's try a some conics for a start
1) A simple
equation would be:
(128-x)^2+((128-y)/2)^2=100
Substracting one thousand makes:
(128-x)^2+((128-y)/2)^2-1000=0
2) Take care here: We know that x^2+y^2/4 is always positive. However now we substracted the squared radius (1000), it may go upto -1000, so we will have to raise to square:
((128-x)^2+((128-y)/2)^2-1000)^2
You can try rendering it now. It will look completely random trash. However if you divide it by e.g. 100, you will see the implicit graph in black.
3) Since we do not know yet how many give to k, let's try e.g. ten:
((128-x)^2+((128-y)/2)^2-1000)^2+10
4 and 5)
2550/(((128-x)^2+((128-y)/2)^2-1000)^2+10)
Render this and you will see that there are only some lonesome pixels. This means that we will have to make k quite bigger:
2550000/(((128-x)^2+((128-y)/2)^2-1000)^2+10000)
Now it is quite nicer.
Replacing the
"+" by a "-" [between the two squared x and y] makes an
hyperbola:
Write it in the green field and let the red like before.
And if you try the opposite (y^2-x^2 instead of x^2-y^2), you will get the other
one:
[I removed here the "/2" to have a more regular picture]
r=2550000/(((128-x)^2+(128-y)^2-1000)^2+10000)
g=2550000/(((128-x)^2-(128-y)^2-1000)^2+10000)
b=2550000/(((128-y)^2-(128-x)^2-1000)^2+10000)

Second example, Descartes' folium:
1) The generic equation is: x3+y3-3axy=0, with a a real number bigger than zero.
As usual, to have our center at (128;128), we shall replace x by (x-128) and y by (y-128):
(x-128)^3+(y-128)^3-3*a*(x-128)*(y-128)
As it require some fine tuning, I give you directely my solution (-:
51000/((((x-128)^3+(y-128)^3)/1000-(x-128)*(y-128)/5)^2+200)
You can have fun putting different k values for each colour component:
r=510000/((((x-128)^3+(y-128)^3)/1000-(x-128)*(y-128)/5)^2+2000)
g=255000/((((x-128)^3+(y-128)^3)/1000-(x-128)*(y-128)/5)^2+1000)
b=25500/((((x-128)^3+(y-128)^3)/1000-(x-128)*(y-128)/5)^2+100)
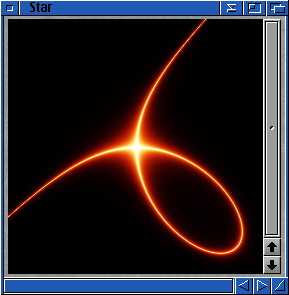
Last example, Bernouilli's Lemniscate:
The generic equation is (x2+y2)2=a2(x2-y2)
Once adapted to our needs (I have set a=100 and k=1000000 and then divided the f(x,y) expression by 1000 to keep small enough numbers), this equation gets:
255000000/((((128-x)^2+(128-y)^2)^2/1000-10*((128-x)^2-(128-y)^2))^2+1000000)

3.1:
Monochrome Graphs
3.2: Implicit functions
3.3: Playing with hyperbolic tangents